Recent searches
Search options
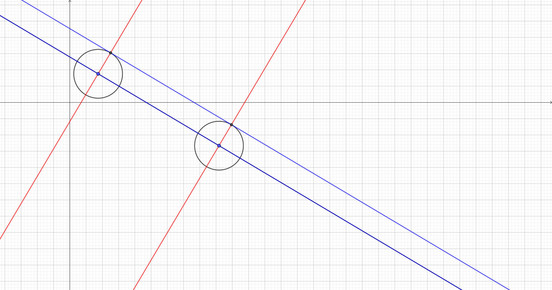
To construct a #ParallelLine to a given line (in blue) in 2D #EuclideanSpace, all you need to do is pick two #points and draw #circles centred at those points of a specified #radius. Draw a #perpendicular to the line at each point (in red) and then draw a new line passing through the intersection of the perpendicular with the circles and there is the line parallel to the original one. Here is the process shown in #Geogebra.
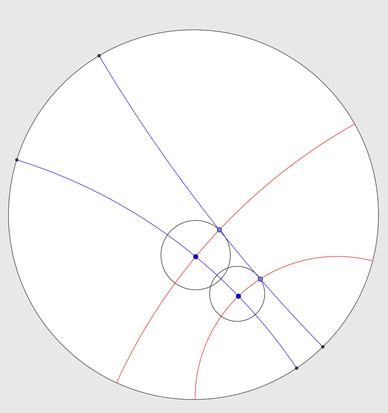
You can also explore #non-Euclidean space and here is the same action in #HyperbolicSpace (here in a #PoincaréDisc). #StraightLines are replaced by #GeodesicLines which look like #CircularArcs which intersect the #disc at #RightAngles. Circles are transformed to circles but their hyperbolic centres are not at their Euclidean centres.
Repeating the construction for Euclidean space, you can see that the parallel lines diverge.